The Floyd-Warshall Algorithm From Graph Theory, Applied to Parsing Molecular Structures | by LucianoSphere (Luciano Abriata, PhD) | Aug, 2024
[ad_1]
Hands-on explanations assisted by simple JavaScript code
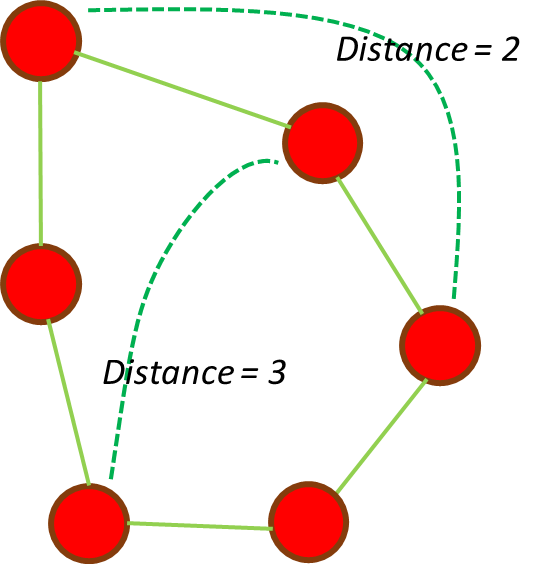
The Floyd-Warshall algorithm is essential in graph theory as it provides an efficient means to compute the shortest paths between all pairs of nodes in a graph. This classic dynamic programming algorithm is widely applicable beyond its traditional use in theoretical network analysis. It works by reading in a matrix that describes which pairs of nodes are connected by a single edge, and outputting the minimal number of edges connecting every possible pair of nodes:
This is precious information about connectivity within the graph, that finds tons of applications; for example in optimizing communication networks, analyzing contacts in social networks, or, as I will cover here, in parsing molecular structures — at the core of many tasks in cheminformatics and structural bioinformatics.
In this post I will show you how the Floyd-Warshall algorithm can be employed to compute bond distances between atoms in a molecule, or said in a different way, the minimal number of bonds separating every possible pair of atoms. Hopefully, my example will not only showcase the algorithm’s application in chemistry but also inspire you to use it for other applications in…
[ad_2]
